Ecuacion
Elementos
construccion
problemas
ELIPSE
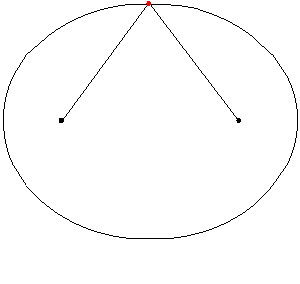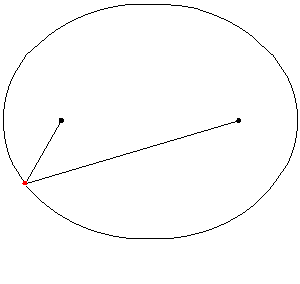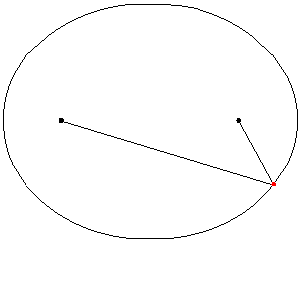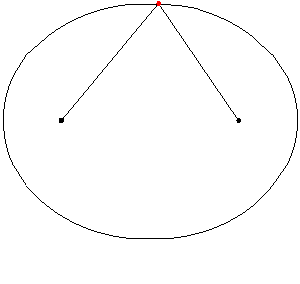
En este link, se enseñara paso a paso la elaboracion de una elipse
*Hallar la ecuación de lugar geométrico de los puntos P(x. y) cuya suma de distancias a los puntos fijos (4, 2) y (−2, 2) sea igual a 8.
* Hallar la ecuación de la elipse de foco F(7, 2), de vértice A(9, 2) y de centro C(4, 2).
ECUACION REDUCIDA
ECUACION DE LA ELIPSE
ECUACION GENERAL
La elipse es una curva plana y cerrada, simétrica respecto a dos ejes perpendiculares entre sí:
-
El semieje mayor (el segmento C-a de la figura), yel semieje menor (el segmento C-b de la figura).
Miden la mitad del eje mayor y menor respectivamente.
PUNTOS DE LA ECLIPSE
Los focos de la elipse son dos puntos equidistantes del centro, F1 y F2 en el eje mayor. La suma de las distancias desde cualquier punto P de la elipse a los dos focos es constante, e igual a la longitud del diámetro mayor (d(P,F1)+d(P,F2)=2a).
Por comodidad denotaremos por PQ la distancia entre dos puntos P y Q.
Directrices de la elipse
La recta dD es una de las 2 directrices de la elipse.
Cada foco F de la elipse está asociado con una recta paralela al semieje menor llamada directriz . La distancia de cualquier punto P de la elipse hasta el foco F es una fracción constante de la distancia perpendicular de ese punto P.
Constante de la elipse
Las longitudes de los segmentos correspondientes a cada uno son PF1 (color azul) y PF2(color rojo), y en la animación se ilustra como varían para diversos puntos P de la elipse.
Como establece la definición inicial de la elipse como lugar geométrico, para todos los puntos P de la elipse la suma de las longitudes de sus dos radio vectores es una cantidad constante igual a la longitud 2a del eje mayor.
Ejes de una elipse
El eje mayor, 2a, es la mayor distancia entre dos puntos opuestos de la elipse. El resultado de la suma de las distancias de cualquier punto a los focos es constante y equivale al eje mayor. El eje menor 2b, es la menor distancia entre dos puntos opuestos de la elipse. Los ejes de la elipse son perpendiculares entre sí.
Excentricidad de una elipse
La excentricidad ε (épsilon) de una elipse es la razón entre su semidistancia focal (longitud del segmento que parte del centro de la elipse y acaba en uno de sus focos), denominada por la letra c, y su semieje mayor. Su valor se encuentra entre cero y uno.
Una elipse es la curva simétrica cerrada que resulta al cortar la superficie de un cono por un plano oblicuo al eje de simetría –con ángulo mayor que el de la generatriz respecto del eje de revolución.1 Una elipse que gira alrededor de su eje menor genera un esferoide achatado, mientras que una elipse que gira alrededor de su eje principal genera un esferoide alargado.
